Technical
AD 306: Additional Moments in Braced Bays: 1
This is the first in a series of ADs that comment on the forces and moments to be designed for in beam-column-bracing connections in braced frames. AD 304 pointed out that the nominal moments that are assumed from beam eccentricity cannot be ignored, even if forces in the bracing system have been calculated from a pin-jointed analysis. This AD covers common connection details and offers advice on how the connections can be designed.
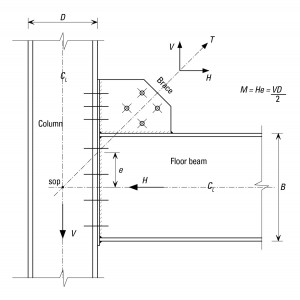
The first common case is where the centre lines of the members are coincident, as shown in Figure 1.
Two models are commonly adopted for the design of the connections shown in Figure 1.
In the first model, the connection to the column is designed for a moment equal to He, where e is the vertical eccentricity from the beam centreline to the point the bracing centreline meets the column flange. Generally, this moment is dealt with by assuming that the point of rotation is the bottom flange of the beam. The vertical shear through the connection is the beam reaction, plus the contribution from the component of the bracing force. If this model is adopted, the nominal moment in the column is due only to the assumed eccentric reaction of the beam shear. There is no contribution from the bracing force to the nominal moment in the column.
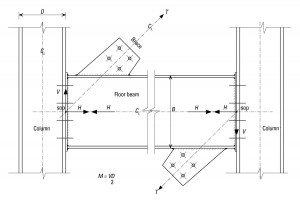
An alternative model is to assume that the bracing is connected to the beam, and that the beam end connection remains truly pinned. In this case the end connection of the beam carries no moment, but must carry the beam shear and the vertical component of the bracing force. The column must be designed for the nominal moment from the assumed eccentric beam shear, plus an additional moment equal to V × D/2 where D is the column depth.
In Figure 2 the setting out point (sop) of the bracing has been shifted to the intersection of the beam centre line with the column face. This is very similar to the second model described above, in that the column must be designed for an additional moment equal to V × D/2. It is also clear from Figure 2 that the vertical component of the bracing force adds to the shear in the beam from gravity loads, and this must be checked. The end connection is designed as a pin, to carry the vertical load from the bracing and the beam itself.
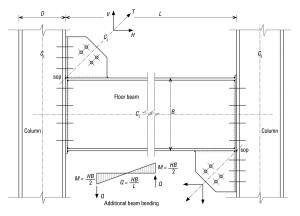
In Figure 3, the common and convenient situation of shifting the sop to the junction of beam and column flanges is shown. The main effect is the additional moment equal to V × D/2 to be included in the column design. Additional shear and bending is produced in the beam, but this is generally not significant. The additional shear and moment is given below.
Additional shear, Q = H × B/L
Additional bending moment, M = H × B/2
Where H is the horizontal component of the bracing force
D is the depth of the column
B is the depth of the beam
L is the span of the beam
In summary, the additional moments that arise in braced bays due to the location of the setting out point must be added to the usual nominal moments from the beam end reactions and accounted for in the design of the column and its splices.
Contact: Thomas Cosgrove
Email: t.cosgrove@steel-sci.com
Tel: 01344 623345