Analysis of composite slabs 

Liam Dougherty of the SCI looks at some of the different approaches that can be used to analyse composite slabs, focusing on the advantages and disadvantages of each approach, particularly in the context of specifications that more and more frequently seem to demand high levels of imposed load.

In the UK, composite slabs are usually analysed as simply supported members in the normal condition (the analysis of the steel sheeting during the construction stage is different), with no account taken of the continuity offered by any reinforced concrete that is continuous over the supports. However, as the concrete of a composite slab floor is typically continuous over the supporting beams, they may be analysed as continuous. Eurocode 4 allows a number of different approaches to analysing a composite slab. 

The analysis of composite slabs is outlined in clause 9.4.2 of BS EN 1994-1-1 which remains unchanged in the second generation of BS EN 1994-1-1. 

In this technical article, three cases are considered:

1. Simply supported.
2. Continuous elastic analysis with redistribution of moments.
3. Continuous plastic analysis.

Simply supported 

Continuous composite slabs can be analysed as simply supported. This approach is outlined in subclause 9.4.2(5) and is acceptable only when nominal reinforcement is provided over intermediate supports. 

For typical composite slab span lengths, the slab will normally fail to achieve the bending resistance predicted by assuming full shear connection (i.e. the sheeting will not yield). The shear bond, which is a function of the contact area between steel and concrete, is likely to be the critical failure mechanism. The bond between the steel and the concrete usually reaches its maximum value at mid-span, as the concrete slips relative to the steel sheeting. The mechanical and frictional interlock that forms the shear connection between the steel and the concrete may be enhanced by end anchorage, such as shear studs on supporting beams, as these also resist slip. Additionally, the bending resistance can be increased by adding reinforcement bars in the troughs irrespective of whether partial shear connection exists.

Determining the bending moment applied to a simply supported composite slab with a uniformly distributed load is straightforward. Movable concentrated loads, for example from MEWPs, would need to be positioned to cause the worst-case bending moment and shear force.

Continuous elastic analysis

Composite slabs can be analysed as continuous using elastic analysis with up to 30% redistribution of hogging moments in accordance with subclause 9.4.2(3). Unlike plastic analysis, the rotational capacity of the composite slab over the supports does not need to be verified provided this limit is respected, as there is a correlation between rotation and redistribution. Reinforcement that is placed over the supports can be used to resist the hogging moment. However, for an efficient design the sagging and hogging resistances should be approximately equal to one another to make full use of the sagging resistance. This would mean adding more reinforcing bars over the supports as the sagging resistance of a typical composite slab in the UK is  substantially greater than its hogging resistance with nominal mesh reinforcement. For typical loading conditions, the additional area of reinforcement required to resist the hogging moment would be greater than if the slab was analysed as simply supported as the sagging resistance would not be fully utilised in the continuous case.

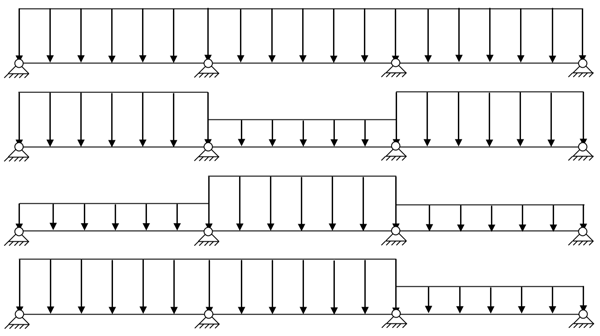
It is worth adding that the analysis of continuous composite slabs is more complex than that for simply supported slabs because numerous loading patterns need to be considered to cause the maximum design sagging and hogging moments as shown in Figure 1. 

The addition of movable concentrated loads is also more complicated in the simply supported condition. 

Continuous plastic analysis

Composite slabs can be analysed as continuous using rigid plastic global analysis where all cross-sections at plastic hinge locations have sufficient rotation capacity. Plastic design is potentially the most efficient approach to maximise the resistance of the composite slab without adding excessive reinforcement over the support.

As with continuous elastic analysis, because of potential interaction between spans the loading may be more complicated than in the simply supported condition and numerous loading patterns may need to be considered. 

In plastic analysis, failure occurs when the limiting rotation at a plastic hinge is reached or when sufficient hinges form to render the structure into a mechanism. Considering an internal span of a composite slab, the capacity can be determined by applying load until the maximum hogging moment at the internal supports is equal to the hogging resistance. Additional loading is then applied until the rotation at the supports reaches the rotational capacity or the bending moment in the span reaches its moment capacity as moment is redistributed into the span from the supports.

The difficulty with this approach is checking that the rotation capacity at the internal supports is sufficient to meet the rotation required. No guidance is given in BS EN 1994-1-1. Although guidance on checking the rotational adequacy is given in clause 5.6.3 of BS EN 1992-1-1, it should only be used for composite slabs with care and justification. In particular, the rules for justifying the rotation capacity based on stress block depth and reinforcement ductility may not be applicable to composite slabs.

Subclause 9.4.2(4) of BS EN 1994-1-1 allows plastic analysis without any check on rotation capacity for continuous composite slabs with spans up to 3.0m using Class C reinforcing steel. This relatively short span limit would suggest that for many typical composite slabs rotation adequacy could well be an issue.

Serviceability

In the UK when calculating deflections composite slabs are typically analysed as simply supported using elastic analysis. 

In accordance with subclause 9.8.2(5), when determining the deflection of a composite slabs for the serviceability limit state, when the slab is either ‘end’ or ‘internal’ the continuity at one or both ends respectively may be taken into account by using an average of the cracked and uncracked second moments of area. 

In the 2012 edition of ‘Designers’ guide to Eurocode 4’ it says that generally, it appears that the redistribution of moments should be avoided in analyses for serviceability limit states.

Therefore, when determining the deflection of continuous composite slabs that are designed with elastic analysis with moment redistribution or with plastic analysis the deflections should be determined using elastic analysis with no moment redistribution. 

Fire stage

Although the free bending moment in the fire condition is equal to the moment that would be calculated assuming simply supported conditions, fire design for composite slabs is based on the combined hogging and sagging plastic resistances of the slab, allowing for continuity over the supports in accordance with clause 4.3.1 of BS EN 1994-1-2. Therefore, the bending resistance of a composite slab in fire will not increase if the designer adopts a continuous approach at ambient.

Example

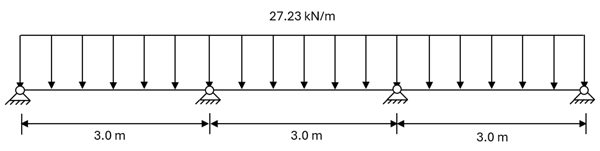
A worked example is now given to illustrate the different approaches. A three-span continuous slab of equal spans of 3.0m. The slab depth is 130mm with trapezoidal steel sheeting with a thickness of 0.9mm and an A252 mesh. As the spans are 3.0m, no check on rotational capacity is required if Class C reinforcement is used. The slab has a uniformly distributed load of 27.23 kN/m as shown in Figure 2. The load is composed of a permanent load of 3.5 kN/m and a variable load of 15.0 kN/m using the combination of actions given in expression 6.10 of BS EN 1990 for simplicity. 

No end anchorage was considered.

Simply supported

The bending moment is shown in Figure 3.

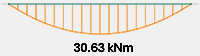
The maximum sagging bending moment occurs at 1.5m.

The sagging resistance with partial shear connection at 1.5m is:

M_Rd = 29.55 kNm

The sagging resistance with an additional Ø 8mm bar in each trough is:

M_Rd = 33.97 kNm

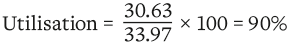
Total deflection = 7.0mm

Allowable deflection = 12.0mm

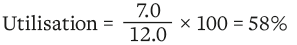
Elastic continuous analysis with 30% redistribution:

The elastic bending moment is shown in Figure 4.

The elastic bending moment with 30% redistribution is shown in Figure 5.

 The hogging resistance with A252 mesh (Ø 8 mm bar at 200mm spacing) is:

M_Rd = 9.31 kNm

As the hogging resistance with an A252 mesh is insufficient, the mesh is replaced with Ø 8mm bars spaced at 100mm spacing.

The hogging resistance with Ø 8mm bar at 100mm spacing is:

M_Rd = 17.05 kNm

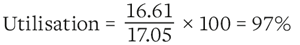
The maximum sagging bending moment is at 1.3m.

The sagging resistance with partial shear connection at 1.3m:

M_Rd = 27.35 kNm

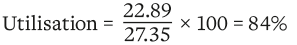
Total deflection = 3.7mm

Allowable deflection = 12.0mm

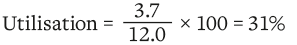
Plastic continuous analysis:

The plastic bending moment is shown in Figure 6.

 The hogging resistance with A252 mesh (Ø 8 mm bar at 200mm spacing) is:

M_Rd = 9.31 kNm

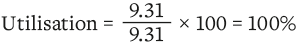
Maximum sagging bending moment is at 1.4m.

Sagging resistance with partial shear connection at 1.4m:

M_Rd = 28.46 kNm

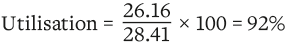
Note that limiting the spans to 3.0m and using Class C reinforcement
(BS EN 1994-1-1, .4.2(4)) avoids the need for a check on rotation adequacy.

Conclusions

The simply supported analysis is the easiest approach in terms of design.

For typical loading conditions, continuous elastic analysis requires more reinforcement overall than in the simply supported condition, as well as more design effort.

The deflection of continuous composite slabs are less than in the simply supported condition.

Whilst plastic analysis could be the most economical approach in terms of material, unless the spans are not greater than 3.0m and Class C reinforcement is used, the rotation capacity must be checked and there is no robust guidance on how to do this. The example has shown that for typical composite slabs, the rotation adequacy could be an issue.